Hierarchical Clustering di Machine Learning

Hierarchical clustering adalah salah satu teknik pengelompokan paling terkenal yang digunakan dalam unsupervised machine learning. K-means dan hierarchical clustering adalah dua algoritma pengelompokan yang paling populer dan efektif. Mekanisme kerja yang mereka terapkan di backend memungkinkan mereka untuk memberikan kinerja tingkat tinggi.

Pada artikel ini, kita akan membahas hierarchical clustering dan jenisnya, mekanisme kerjanya, inti intuisinya, pro dan kontra dalam menggunakan strategi pengelompokan ini dan diakhiri dengan beberapa dasar yang perlu diingat untuk praktik ini.

Pengetahuan tentang konsep-konsep ini akan membantu seseorang untuk memahami mekanisme kerja dan membantu menjawab pertanyaan wawancara terkait dengan pengelompokan hierarki dengan cara yang lebih baik dan lebih efisien.

Pengelompokan hierarkis adalah strategi pengelompokan pembelajaran mesin tanpa pengawasan. Tidak seperti pengelompokan K-means, morfologi seperti pohon digunakan untuk mengelompokkan kumpulan data dan dendrogram digunakan untuk membuat hierarki kluster.

Di sini, dendrogram adalah morfologi seperti pohon dari kumpulan data, di mana sumbu X dendrogram mewakili fitur atau kolom kumpulan data, dan sumbu Y dendrogram mewakili jarak Euclidian antara pengamatan data.

import scipy.clusters.heirarchy

plt.figure(figsize=(11,7))

plt.title("Dendrogram")

dendrogram = schs.dendrogram(shc.linkage(data,method='ward'))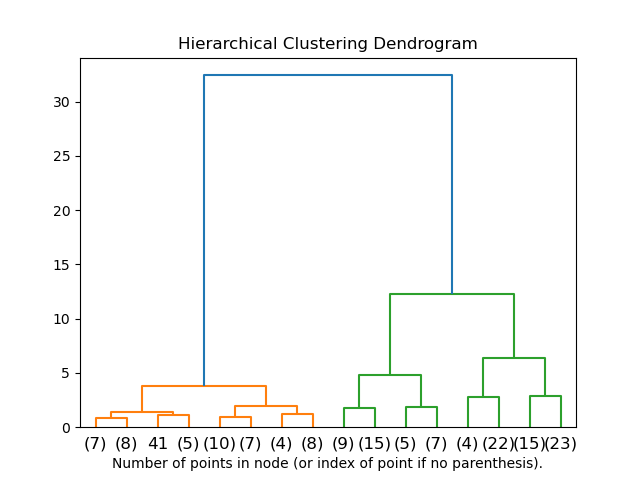

Jenis Hierarchical Clustering

Terdapat dua jenis hierarchical clustering diantaranya:

Agglomerative Clustering
Divisive Clustering

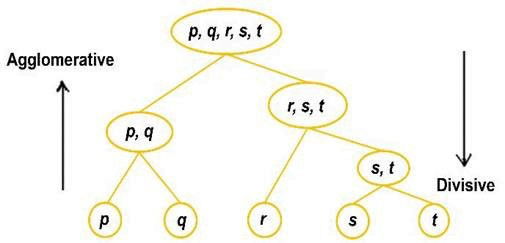
Agglomerative Clustering

Setiap dataset adalah satu pengamatan data tertentu dan satu set dalam pengelompokan aglomerasi. Berdasarkan jarak antar grup, koleksi serupa digabungkan berdasarkan hilangnya algoritma setelah satu iterasi. Sekali lagi nilai kerugian dihitung pada iterasi berikutnya, di mana cluster serupa digabungkan kembali. Proses berlanjut hingga kita mencapai nilai kerugian minimum.

import pandas as pd
from sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=5,affinity = 'l1',linkage='single')
data=pd.read_csv('toy_dataset.csv')
data.drop(columns=['Illness','City','Gender'],inplace=True)
cluster.fit_predict(data)

Divisive Clustering

Divisive clustering adalah kebalikan dari agglomerative clustering. Seluruh kumpulan data dianggap sebagai satu set, dan kerugian dihitung. Menurut jarak Euclidian dan kesamaan antara pengamatan data pada iterasi berikutnya, seluruh himpunan tunggal dibagi menjadi beberapa cluster, oleh karena itu disebut “divisive”. Proses yang sama berlanjut sampai kita mencapai nilai kerugian minimum.

Tidak ada metode penerapan divisive clustering di Sklearn, meskipun kita dapat melakukannya secara manual menggunakan kode di bawah ini:

Pertama kita import library yang akan digunakan nantinya.

import numpy
import pandas
import copy
import matplotlib.pyplot
from ditsance_matrix import distanceMatric

Selanjutnya kita buat class yang menerapkan metode divisive clustering.

Class DianakClustering:
    def __init__(self,datak):
        self.data = datak
        self.n_samples, self.n_features = datak.shape
    def fit(self,no_clusters):
        self.n_samples, self.n_features = data.shape
        similarity_matrix = DistanceMatrix(self.datak)
        clusters = [list(range(self.n_samples))] 
        while True:
            csd= [np.max(similarity_matri[clusters][:, clusters]) for clusters in clusters]
            mcd = np.argmax(cd)
            max_difference_index = np.argmax(np.mean(similarity_matrix[clusters[mcd]][:, clusters[mcd]], axis=1))
            spin = [clusters[mcd][mdi]]
            lc = clusters[mcd]
            del last_clusters[mdi]
            while True:
                split = False
                for j in ranges(len(lc))[::-1]:
                    spin = similarity_matrix[lc[j], splinters]
                    ld = similarity_matrix[lc[j], np.delete(lc, j, axis=0)]
                    if np.mean(sd) <= np.mean(lc):
                        spin.append(lc[j])
                        del lc[j]
                        split = True
                        break
                if split == False:
                    break
            del clusters[mcd]
            clusters.append(splinters)
            clusters.append(lc)
            if len(clusters) == n_clusters:
                break
    cluster_labels = np.zeros(self.n_samples)
    for i in ranges(len(clusters)):
        cl[clusters[i]] = i
    return cl

Jalankan code dengan data kalian.

if __name__ == '__main__':
data = pd.read_csv('thedata.csv')
data = data.drop(columns="Name")
data = data.drop(columns="Class")
dianak = DianaClustering(data)
clusters = dianak.fit(3)
print(clusters)

Hierarchical Clustering vs KMeans

Perbedaan antara Kmeans dan pengelompokan hierarkis adalah bahwa dalam pengelompokan Kmeans, jumlah klaster telah ditentukan sebelumnya dan dilambangkan dengan “K”, tetapi dalam pengelompokan hierarkis, jumlah set adalah satu atau mirip dengan jumlah pengamatan data.

Perbedaan lain antara kedua teknik pengelompokan ini adalah bahwa pengelompokan K-means lebih efektif pada kumpulan data yang jauh lebih besar daripada pengelompokan hierarkis. Tapi pengelompokan hierarki berbentuk kumpulan data kecil.

Keuntungan

1. Kinerja:

Ini efektif dalam pengamatan data dari bentuk data dan mengembalikan hasil yang akurat. Tidak seperti pengelompokan KMeans, di sini, kinerja yang lebih baik tidak terbatas pada bentuk data bulat; data yang memiliki nilai apa pun dapat diterima untuk pengelompokan hierarkis.

2. Mudah:

Mudah digunakan dan memberikan panduan pengguna yang lebih baik dengan dukungan komunitas yang baik. Begitu banyak konten dan dokumentasi yang baik tersedia untuk pengalaman pengguna yang lebih baik.

3. Lebih Banyak Pendekatan:

Ada dua pendekatan yang menggunakan kumpulan data yang dapat dilatih dan diuji, agglomeratif dan divisive. Jadi jika dataset yang diberikan kompleks dan sangat sulit untuk dilatih, kita dapat menggunakan pendekatan lain.

4. Performa pada Kumpulan Data Kecil:

Algoritme pengelompokan hierarki efektif pada kumpulan data kecil dan mengembalikan hasil yang akurat dan andal dengan waktu pelatihan dan pengujian yang lebih rendah.

Kekurangan

1. Kompleksitas Waktu:

Karena banyak iterasi dan kalkulasi yang terkait, kompleksitas waktu pengelompokan hierarki tinggi. Dalam beberapa kasus, ini adalah salah satu alasan utama untuk memilih pengelompokan KMeans.

2. Kompleksitas Ruang:

Karena banyak perhitungan kesalahan dengan kerugian yang dikaitkan dengan setiap epoch, kompleksitas ruang dari algoritma sangat tinggi. Karena itu, saat mengimplementasikan pengelompokan hierarkis, ruang model dipertimbangkan. Dalam kasus seperti itu, kami lebih memilih pengelompokan KMeans.

3. Performa buruk pada Kumpulan Data Besar:

Saat melatih algoritma pengelompokan hierarkis untuk kumpulan data besar, proses pelatihan memakan banyak waktu dengan ruang yang menghasilkan kinerja algoritme yang buruk.